
where use has been made of Equation (457), and some standard vector identities (see. A massless string, with an object of mass m 0. The total angular momentum of the body (about the origin) is written. A steel washer is mounted on a cylindrical rotor of radius r 12.7 mm. Hint: Use the moment of inertia of the whole system, Itotat acquired from letter a, then use: L = lw.Consider a point-like particle of mass m moving with a velocity \(\overrightarrow\) direction if you use polar coordinates). Example 17.11 Experimental Method for Determining Moment of Inertia. The motion goes through a complete circle in a period of about 26,000 years. Calculate the total angular momentum of the system. The rotational axis of the Earth is tilted with respect to the normal to. Hint: Compute for the moment of inertia of the child (Ichita = mchita™m³) and the of inertia of the merry-go-round moment (moment of inertia for a solid disc is mr² so Im =mmFm*) first then compute for the sum, Irotal = Ichita + Im- %3D b. In this video David explains more about what moment of inertia means, as well as giving the moments of inertia for commonly shaped objects. Calculate the moment of inertia of the system about its axis of symmetry. If it experiences a torque of 15-Nm for 10-s, what is its final angular speed Given: Moment of inertia of object: I 40 kgm 2 Initial angular speed of object: i 0 rad / s Torque on object: 15 Nm. Assume that you can treat the child as a point particle and you can model the merry-go-round as a disc. A circular object has a moment of inertia of 40 kgm 2 about its center and is initially at rest. The mass and the radius of the merry-go-round are 85 kg and 8 m, respectively. We want to find r, the radius of the string when the particle has a speed of 20 m/s. In addition, the initial moment of inertia of the particle is I o mR 2 4m. A 35-kg child is sitting along the rim of a merry-go- round that is rotating at 0.35 revolutions per second about its symmetry axis. Thus the initial angular velocity of the particle is o v/r 3 rad/s. %3D Moment Of Inertia and Angular Momentum 3. Hint: Use the moment of inertia of the whole system, Itotat acquired from letter a, then use: L = lw. Calculate the total angular momentum of the system.
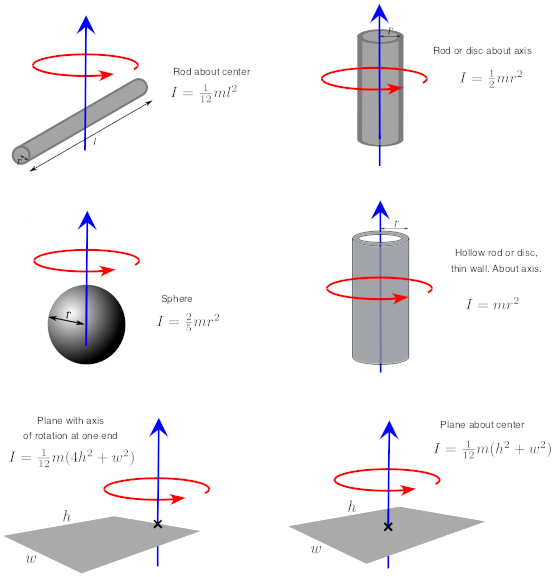
Hint: Compute for the moment of inertia of the child (Ichita = mchita™m³) and the of inertia of the merry-go-round moment (moment of inertia for a solid disc is mr² so Im =mmFm*) first then compute for the sum, Irotal = Ichita + Im- %3D b.
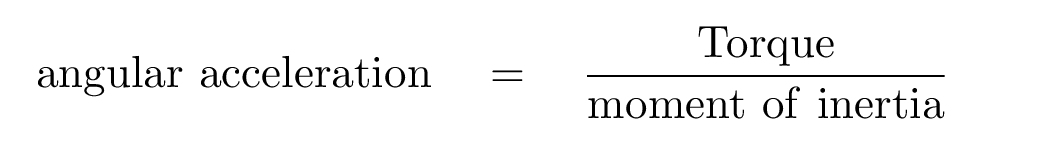
Angular momentum is conserved when the radius of the circle is changed.

A bug standing on the axis decides to crawl out to the other end of the rod. The rod has an angular velocity of 0.33 rad/s and a moment of inertia of 1.40 10-3 kg

The axis is perpendicular to the length of the rod at one of its ends. Assume that you can treat the child as a point particle and you can model the merry-go-round as a disc. Experiments Using the ME-8953 Rotational Inertia Accessory. A thin rod has a length of 0.25 m and rotates in a circle on a frictionless tabletop. A 35-kg child is sitting along the rim of a merry-go- round that is rotating at 0.35 revolutions per second about its symmetry axis. I can figure out the platforms moment of intertia. I figure that it would just be the sum of the moments of intertia of the platform and the student.
#Angular moment of inertia of a circle how to
Science Physics Q&A Library Moment Of Inertia and Angular Momentum 3. I need to know how to figure out the moment of inertia of a system that consists of a spinning circular platform with a student standing still on the platform.


 0 kommentar(er)
0 kommentar(er)
